Factoring expressions

The problem with the previous resistor model, extended from the component model, which itself consists of two ports, is that the current in the resistor is represented by three variables: I, Pin.I, Pin.out. Conceptually, these three variables form a single variable. In fact, I is the only real unknown for the current flowing through the resistor. Pin.I and Pout.i are deduced causally from I. To express this, we will declare the variable I in the Port model as an expr as foolow:

Model Port()
Constants

Variables
V : Voltage ;

expr I : Current ;

Elements

Properties

End

An expr can be used to name any algebraic expression. The definition will be made here in the Dipole model using the := operator as follow:

Model Dipole (index)
Constants
index : DipoleIndex ;

Variables
I :  Current;

Elements
Pin : Port();
Pout : Port() ;

Properties
Pin.I :=  I;
Pout.I := -I;

End

Note

All the expr of a DEPS problem must necessarily form a Direct Acyclic Graph (DAG). No circularity is possible between expr. Moreover an expr is defined once and only once in a problem.

A zipfile containing the whole DEPS project OneResistorWithExpr.proj described in this section can be downloaded via this link .

After opening the OneResistorWithtExpr.proj project file in DEPS Studio, we can compile the project (project > build the problem).

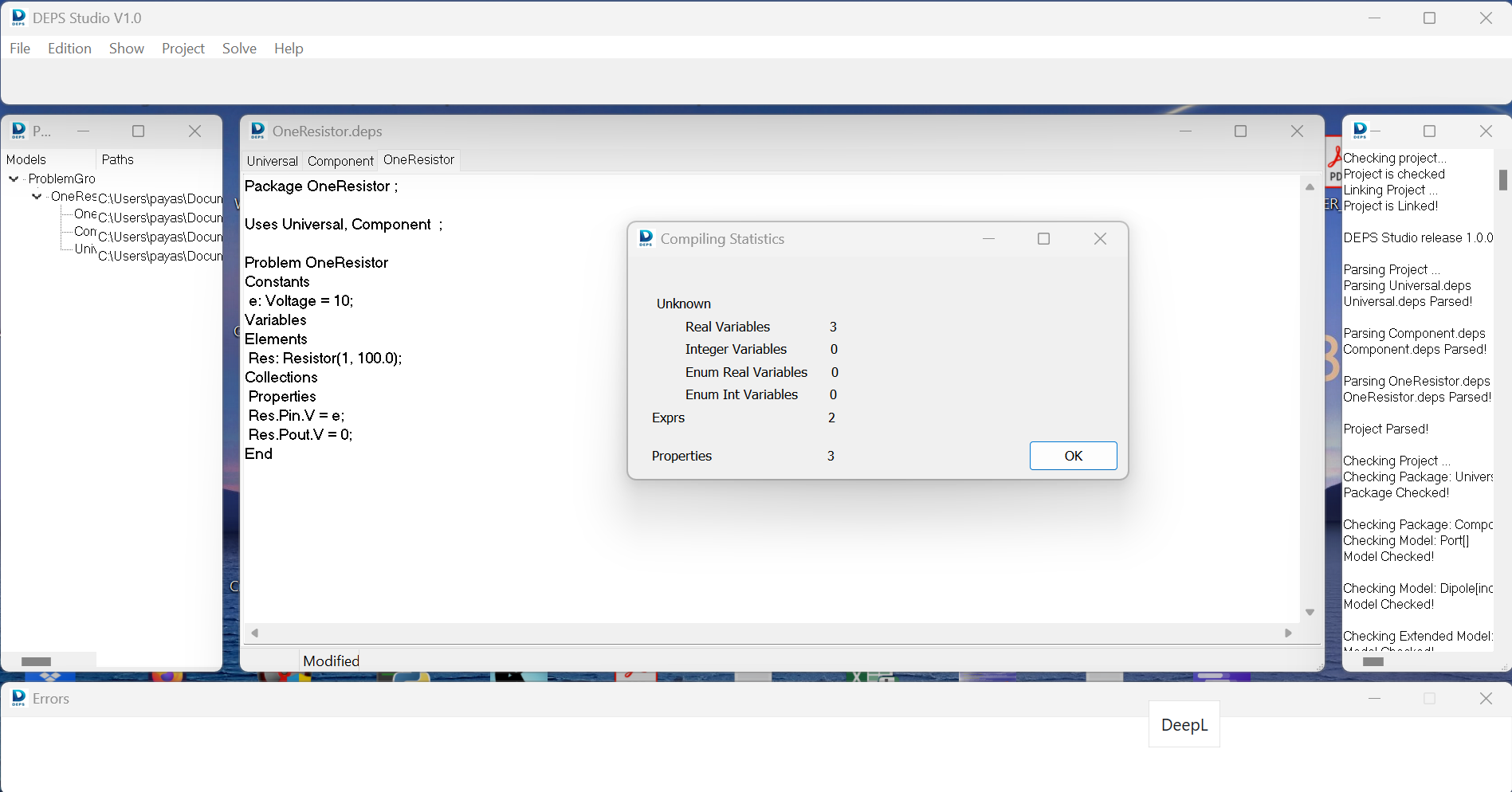
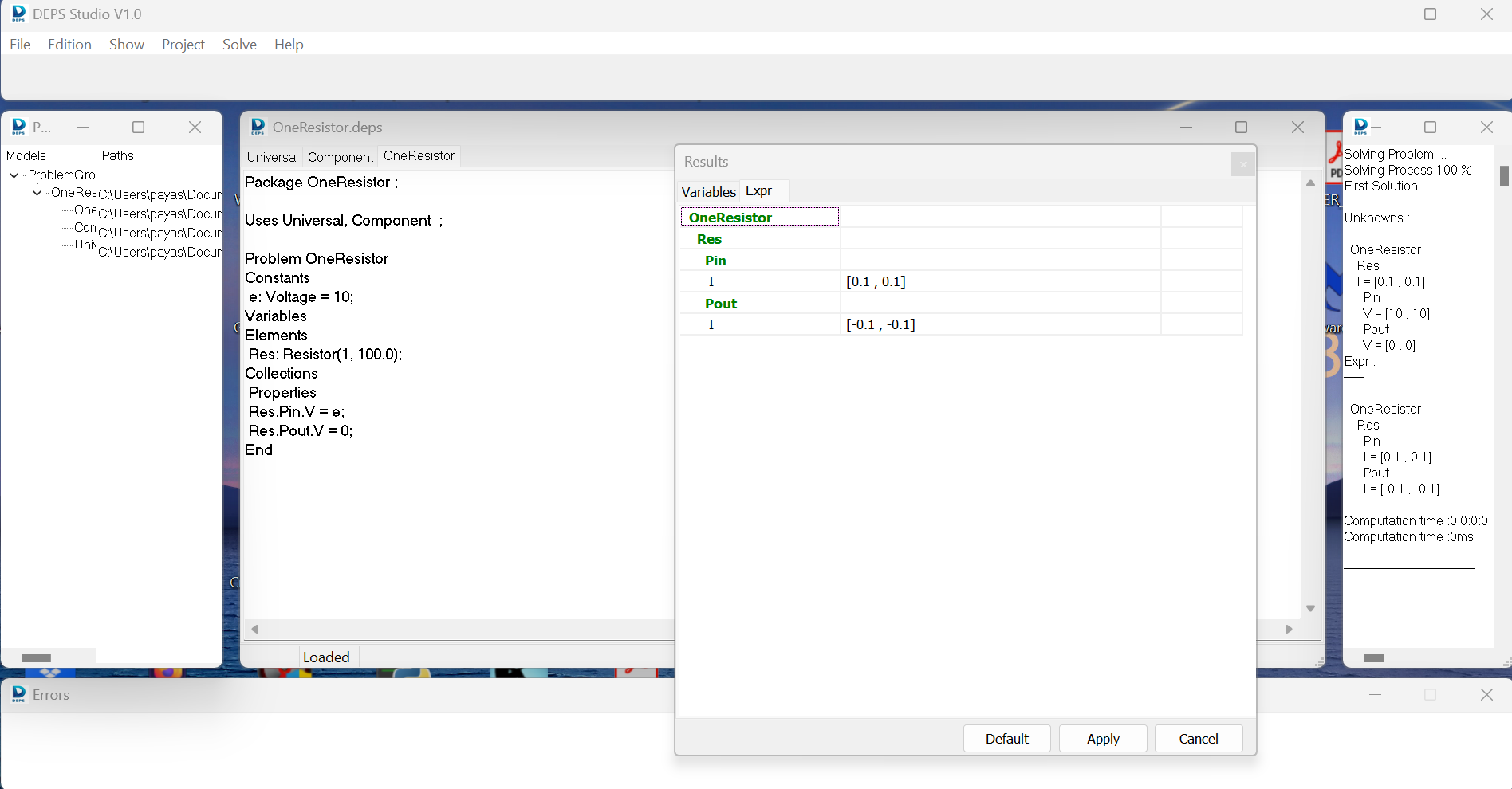
Comparing to the previous model (without expr) we see that now we have 3 variables and 2 expr rather than 5 variables.

Then the problem can be solved (Solve > First Solution).

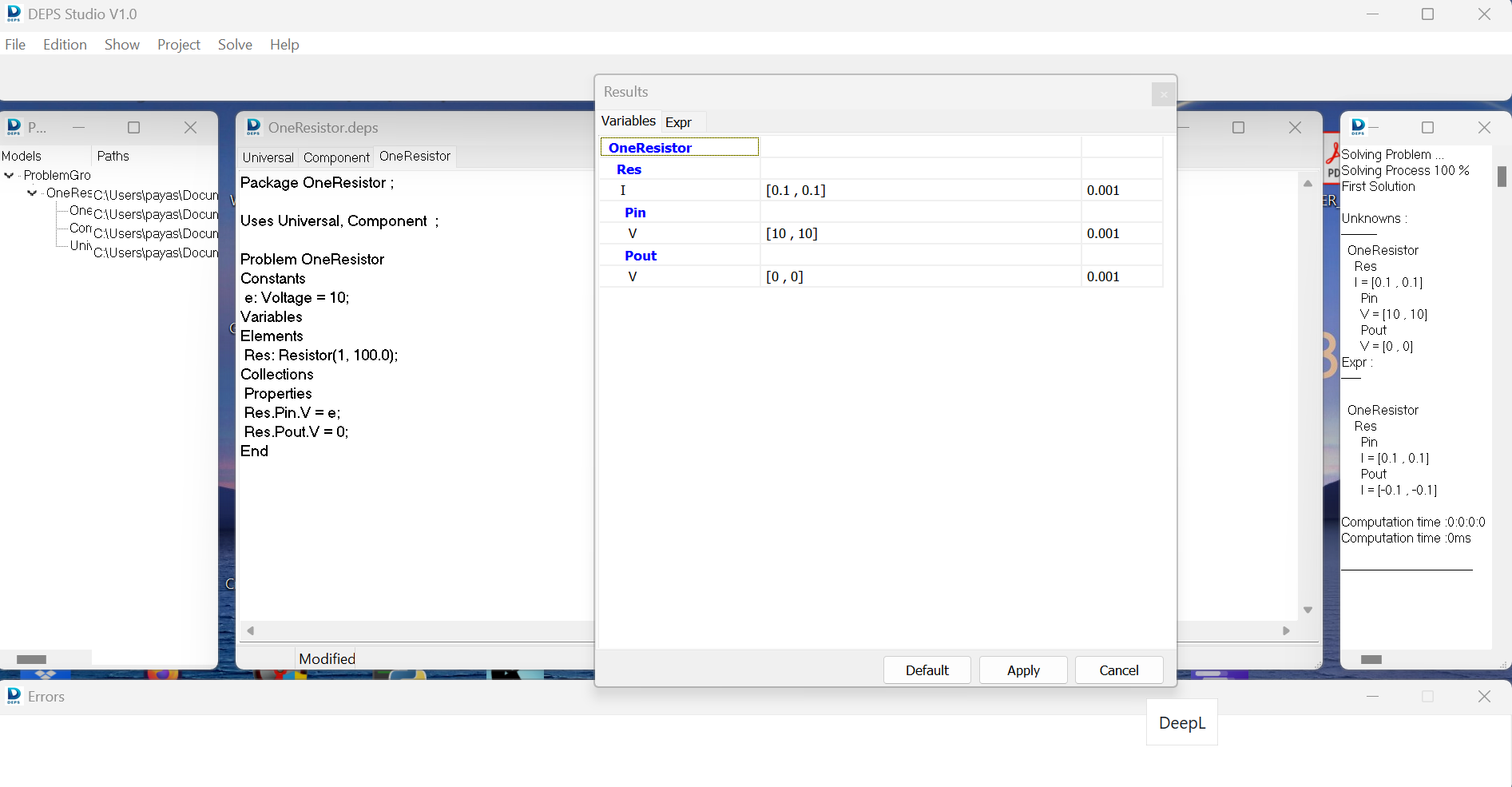
We can have a look to the expr values too: