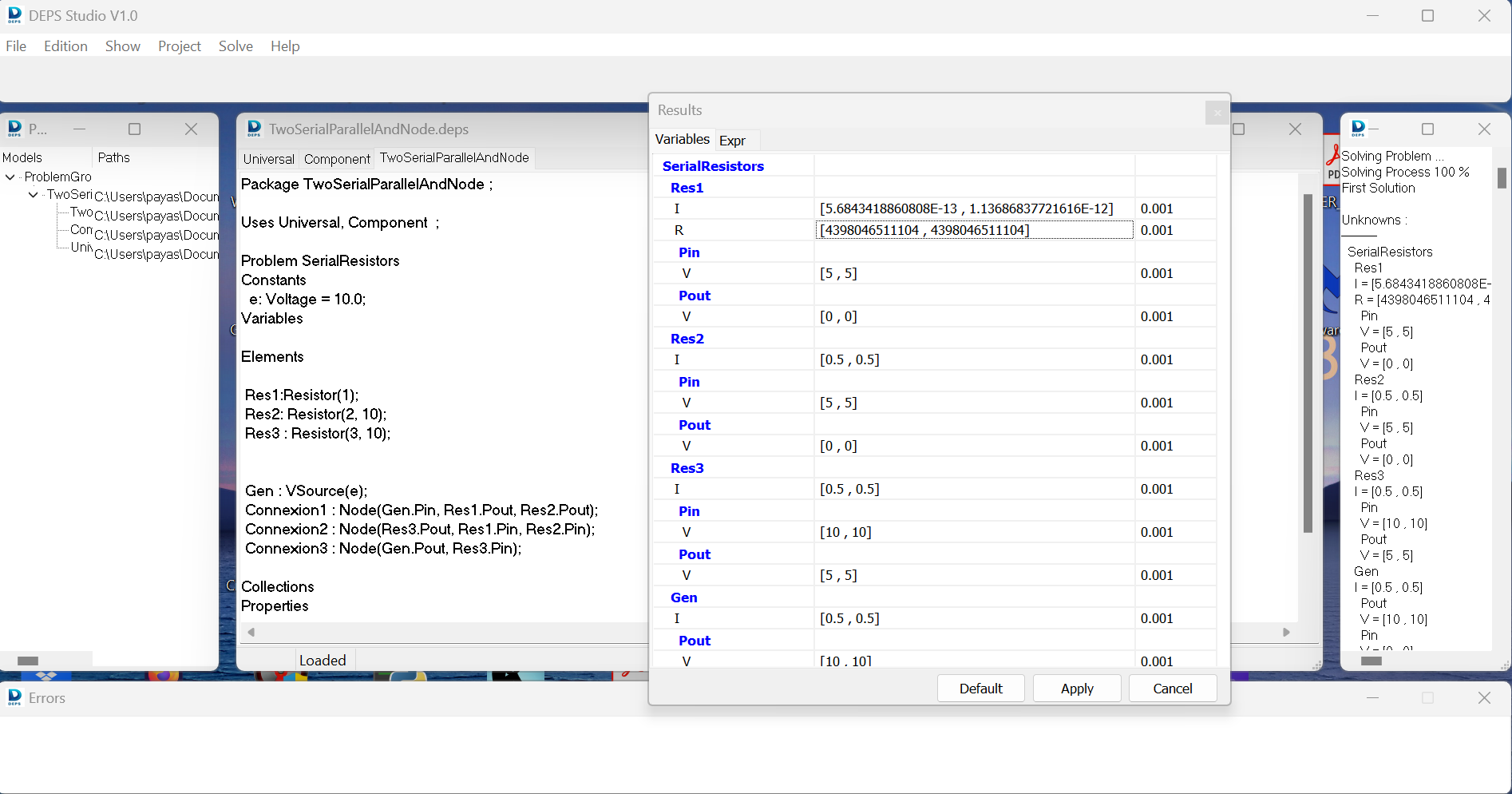
A more complicated problem: serial and parallel circuit

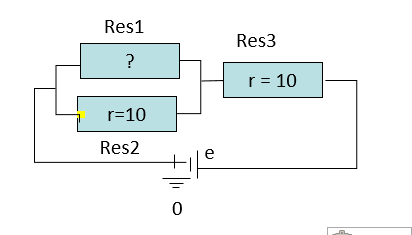
Here we are trying to model an electrical circuit in which two resistors, one known, the other unknown, are connected in parallel and linked with another kwon resistor in series. The whole system is connected to a voltage generator with an imposed current. The problem is to find the value of Res1 such that the current in the circuit is equal to 0.5 A.

Modeling ternary node

If we look at the picture, we see that we need a binary node model and a ternary node model.

Model Node (P1,P2)
Constants

Variables

Elements
P1 : Port[];
P2 : Port[];

Properties
P1.V = P2.V ;
P1.I+P2.I = 0 ;

End

Based on the previous binary node model, it is easy to build a ternary node model as follow:

Model Node (P1,P2, P3)
Constants

Variables

Elements
P1 : Port[];
P2 : Port[];
P3 : Port[];

Properties
P1.V = P2.V ;
P2.V = P3.V ;
P3.V = P1.V ;
P1.I+P2.I+P3.I = 0 ;

End

Modeling generators

All the system components will be connected to each other via ports. It is therefore necessary to have a generator model based on input and output ports. First of all, we will create a battery model called VSource with voltage as a parameter (e). A current (I) to be calculated as a function of the load will flow through the battery. The model below follows the receiver convention with an input port (P2) and an output port (P1).

Model VSource(e)
Constants
e : Voltage;
Variables
I : Current;

Elements
Pin : Port();
Pout: Port();

Properties
Pout.V = e;
Pin.V = 0;
Pout.I := -I;
Pin.I :=I;

End

But we can do better to move towards greater genericity. If we create a very general model of a generator, we can then derive other more specialised generator models from this model, in particular our new parameterised VSource model.

Model Generator()
Constants
Variables
I : Current;
expr e : Voltage;
Elements
Pout: Port();
Pin : Port();

Properties
e := Pout.V-Pin.V;
Pout.V = e;
Pin.V = 0;
Pout.I := -I;
Pin.I :=I;
End

Model VSource(U) extends Generator[]
Constants
U : Voltage;
Variables

Elements

Properties
e = U;

End

Modeling the problem

So we have models of parameterised resistance, unknown resistance and parameterised voltage source. We have also previously established binary and ternary node models.

Problem TwoSerialParalellAndNode
Constants
e : Voltage = 10;

Variables

Elements
Gen : Vsource(e);
Res1 : Resistor(1) ;
Res2 : Resistor(2, 10) ;
Res3 : Resistor(3, 10) ;

Connexion1 : Node(Gen.Pin, Res1.Pout, Res2.Pout);
Connexion2 : Node(Res3.Pout, Res1.Pin, Res2.Pin);
Connexion3 : Node(Gen.Pout, Res3.Pin);

Properties
Res3.I = 0.5;

End

Compiling and solving

A zipfile containing the whole DEPS project TwoSerialParallelAndNode.proj described in this section can be downloaded via this link .

After opening the TwoSerialParallelAndNode.proj project file in DEPS Studio, we can compile the project (project > build the problem).

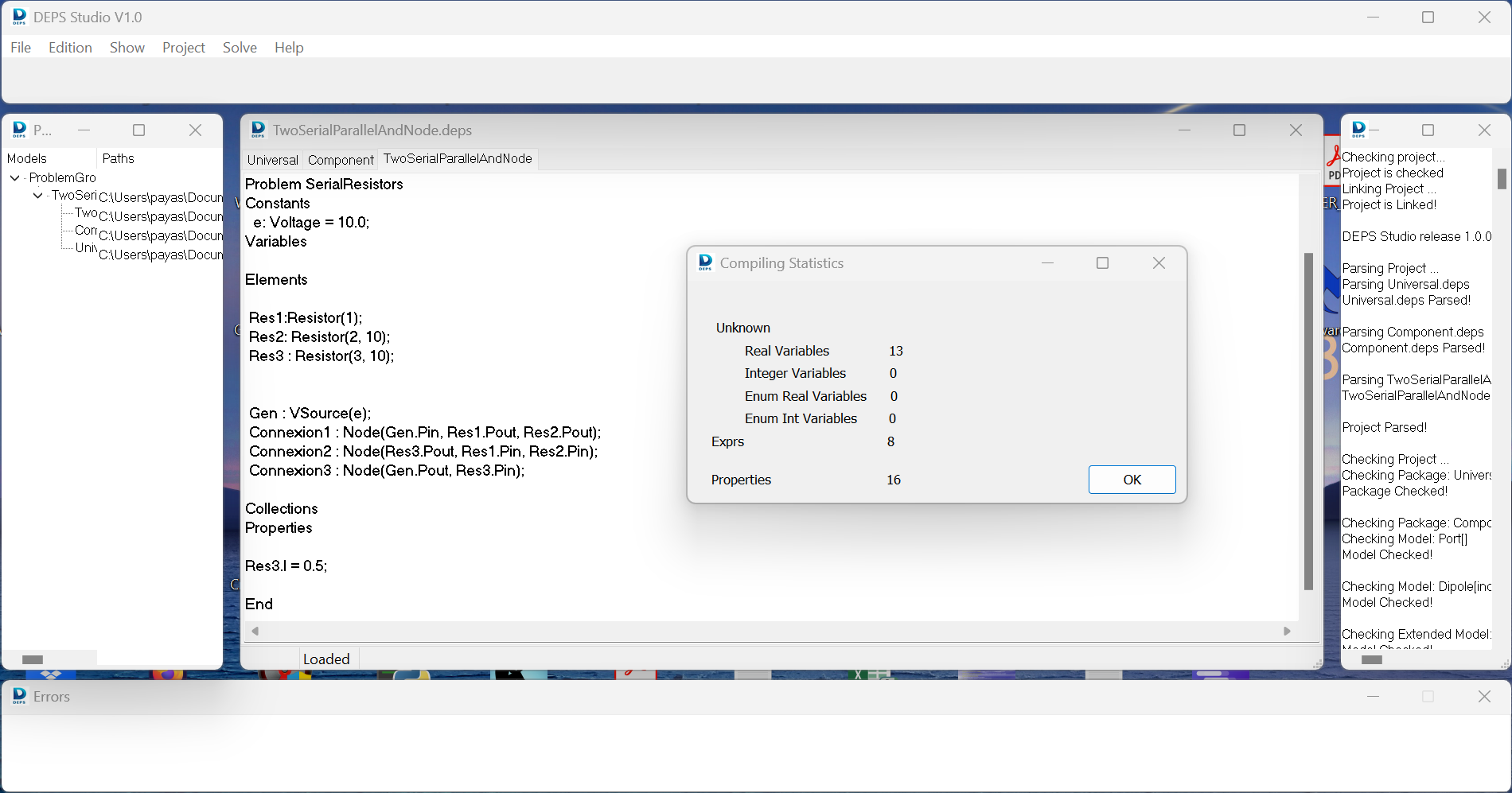
Then the problem can be solved (Solve > Firts Solution).